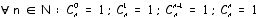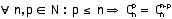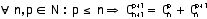# .

Analyse Combinatoire

Introduction

De combien de manières je peux choisir un délégué dans cette classe?
De combien de manière je peux choisir deux délégués de cette classe (un garçon et une fille)?

Tiercé, lotto, ...

Dénombrement

Définition:
1) Si A est un ensemble fini, alors le nombre d’éléments de cet ensemble est appelé le cardinal de l’ensemble et est noté #A.

2) Deux ensembles A et B sont équipotents
SSI
ils contiennent le même nombre d’éléments.

Exemple : A = l’ensemble des élèves de la classe
# A = 21

Cardinal de la réunion de deux ensembles:
1) Si les ensembles A et B sont disjoints,
alors #(A B) = # A + # B

2) Si les ensembles A et B ne sont pas disjoints,
alors #( A B) = # A + # B - #(A B)

Produit cartésien d’ensembles:
+ Le produit cartésien de deux ensembles A et B, noté A x B, est l’ensemble des couples dont la première composante appartient à A et la seconde composante appartient à B.
A x B = { (x , y) | x A et y B }

+ Le produit cartésien de n ensembles A1 , A2 , . . . , An , noté A1 x A2 x . . . x An , est l’ensemble des n-uples dont la première composante appartient à A1 , la deuxième à A2 , . . . , la n-ième à An.
A1 x A2 x . . . x An = { (a1, a2, . . . , an) | a1 A1 , a2 A2 , . . . , an An }


Cardinal d’un produit cartésien:
Exemple: Choix d’un couple de délégués dans une classe : cardinal de G x F ?

+ Le cardinal du produit cartésien d’un nombre fini d’ensembles finis est égal au produit des cardinaux de ces ensembles
#( A1 x A2 x . . . x An) = #( A1) . #(A2 ) . . . #(An)

Exemple: Combien peut-on former de mots de trois lettres dont la première et la troisième sont des consonnes et la deuxième lettre est une voyelle?
#(C x V x C) = 20 . 6 . 20 = 2400


Dénombrement par comptage direct:
Exemples:
De combien de manières peut-on classer 3 personnes par ordre de préférence?
Combien peut-on former de «mots» de trois lettres?
Combien peut-on former de numéros de téléphone de 7 chiffres?


Arrangements à répétition :
Définition:
Tout arrangement à répétition de n objets pris p à p est une liste de p objets, distincts ou non, choisis parmi les n objets donnés; deux listes pouvant différer soit par la nature des éléments, soit par l’ordre des éléments.
Le nombre d’arrangements à répétition de n objets pris p à p est noté .

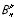Formule:
.

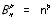Exemples: Combien peut-on former de numéros de téléphone de 7 chiffres?
Trouver un autre exemple.

Interprétation en termes de tirages dans une urne
L’ensemble des n objets proposés devient une urne contenant n boules numérotées de 1 à n.
On effectue p tirages successifs avec remise, l’ordre du tirage étant pris en considération.
Le nombre de possibilités de tirer, dans un ordre donné, avec remise, p boules dans une urne contenant n boules numérotées de 1 à n est 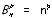, c’est-à-dire le nombre d’arrangements à répétition de n objets pris p à p.

Arrangements sans répétition
Définition:
Tout arrangement sans répétition de n objets pris p à p est une liste de p objets distincts choisis parmi les n objets distincts donnés, deux listes différant soit par la nature des éléments soit par leur ordre.

Le nombre d’arrangements sans répétition de n objets pris p à p est noté .

Exemple: De combien de manières peut-on choisir 3 délégués parmi 5 candidats en indiquant un ordre de préférence?
Formule:
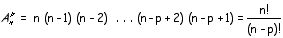(n plus grand ou égal à p)

Exemple: De combien de manières différentes 14 élèves peuvent-ils former une équipe de football, si l’on indique la place que doit occuper chaque joueur? 14529715200

Interprétation en termes de tirages dans une urne
L’ensemble des n objets proposés devient une urne contenant n boules numérotées de 1 à n.
On effectue p tirages successifs sans remise, l’ordre du tirage étant pris en considération.
Le nombre de possibilités de tirer, dans un ordre donné, sans remise, p boules dans une urne contenant n boules numérotées de 1 à n est 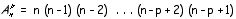, c’est-à-dire le nombre d’arrangements sans répétition de n objets pris p à p.


Permutations sans répétition
Définition:
Toute permutation sans répétition de p objets est une liste de p objets distincts C’est donc une permutation d’un ensemble de p éléments.

Le nombre de permutations sans répétition de p objets est noté PP.

Exemple: Combien de nombres différents de trois chiffres peut-on construire avec les chiffres 1, 2 et 3?
Formule:


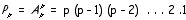
Exemple: De combien de manières différentes 11 élèves peuvent-ils former une équipe de football, si l’on indique la place que doit occuper chaque joueur? 39916800


Dénombrement par comptage indirect:
Exemple:
De combien de manières peut-on choisir 3 personnes parmi 5?


Combinaisons sans répétition :
Définition:
Toute combinaison sans répétition de n objets pris p à p est une liste de p objets distincts choisis parmi les n objets donnés; deux listes différant uniquement par la nature des éléments.
Le nombre de combinaisons sans répétition de n objets pris p à p est noté .

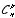Formule:


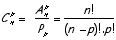
Exemple: De combien de manières 14 élèves peuvent-ils former une équipe de football, sans indiquer la place occupée par chacun d’eux?

Interprétation en terme de tirages dans une urne
L’ensemble des n objets proposés devient une urne contenant n boules numérotées de 1 à n.
On effectue p tirages successifs sans remise, l’odre du tirage n’étant pas pris en considération.
Le nombre de possibilités de tirer p boules sans remise dans une urne contenant n boules numérotées de 1 à n en ne tenant pas compte de l’ordre est
.

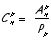Exemple: 7 chevaux sont au départ d’une course. Combien y a-t-il de tiercés possibles dans le désordre?

Propriétés des combinaisons
1)

2)

3)

4) Triangle de Pascal



ANALYSE COMBINATOIRE : Exercices

1) 7 acteurs présentent une pièce comportant 7 rôles différents. De combien de manières peut-on faire la distribution?
2) Une pièce de théâtre se présente comme un dialogue entre un homme et une femme. Comment faire le choix si la troupe se compose de 5 hommes et six femmes?
3) Lors d’un concours, 3 prix différents sont distribués et 20 personnes ont participé. De combien de façons peut-on répartir les 3 prix si une même personne peut éventuellement emporter plusieurs prix?
4) Même question si une même personne ne peut recevoir qu’au plus un prix.
5) Combien de «mots» de 3 lettres peut-on former avec les lettres du mot «FORET»?
6) Même question en utilisant toutes les lettres.
7) Un régisseur de théâtre doit composer une équipe de trois éclairagistes en choisissant parmi 10 candidats. Combien de choix différents peut-il faire?
8) Lors d’un héritage, on doit répartir 3 beaux meubles différents entre les 5 enfants du défunt. De combien de façons peut-on faire la distribution si chaque enfant ne reçoit pas plus d’un meuble?
9) Même question si un enfant peut recevoir plusieurs meubles.
10) Combien y a-t-il de de nombres paires de 4 chiffres?
11) Dans une classe de 10 élèves, les professeurs désirent attribuer un prix d’excellence, un prix du travail et un prix de politesse (rien n’interdit qu’un même élève ait plusieurs prix). De combien de façons peuvent-ils faire leur choix?
12) Même question s’il est hors de question que l’élève A ait le prix du travail.
13) De combien de manières différentes une société de 10 membres peut-elle choisir un groupe de 3 membres pour effectuer un voyage?
14) De combien de manières différentes une société de 10 membres peut-elle élire un président, un secrétaire et un trésorier?

Analyse Combinatoire
F. Mélotte – Collège Saint-Pierre à Uccle